Как рассчитать средний коэффициент

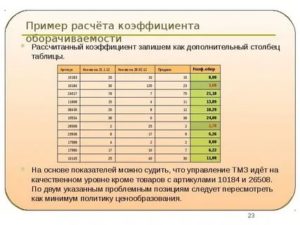
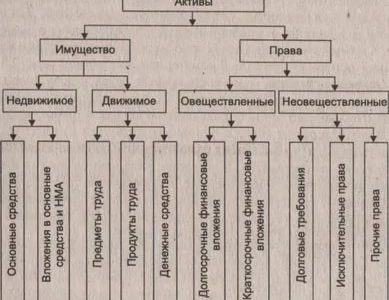
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.

В чем проблема?

Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.

Давайте обратимся к классическому примеру со средней зарплатой.

В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).

Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

• x – среднее арифметическое;
• xn – конкретное значение;
• n – количество значений.

Плюсы:

• Хорошо работает при нормальном распределении значений в выборке;
• Легко вычислить;
• Интуитивно понятно.

Минусы:

• Не дает реального представления о распределении значений;
• Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

• M0 – мода;
• x0 – нижняя граница интервала, который содержит моду;
• n – величина интервала;
• fm– частота (сколько раз в ряду встречается то или иное значение);
• fm-1 – частота интервала предшествующего модальному;
• fm+1 – частота интервала следующего за модальным.

Плюсы:

• Прекрасно подходит для получения представления об общественном мнении;
• Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
• Проста для понимания.

Минусы:

• Моды может просто не быть (нет повторов);
• Мод может быть несколько (многомодальное распределение).

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

• Me – медиана;
• x0 – нижняя граница интервала, который содержит медиану;
• h – величина интервала;
• f i – частота (сколько раз в ряду встречается то или иное значение);
• Sm-1 – сумма частот интервалов предшествующих медианному;
• fm – число значений в медианном интервале (его частота).

Плюсы:

• Дает самую реалистичную и репрезентативную оценку;
• Устойчива к выбросам.

Минусы:

• Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

• СРЗНАЧ(число1;[число2];…) — функция для определения среднего арифметического;
• МОДА.ОДН(число1;[число2];…) — функция моды (в более старых версиях Excel использовалась МОДА(число1;[число2];…));
• МЕДИАНА(число1;[число2];…) — функция для поиска медианы.

И вот какие значения у нас получились:

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

https://www.youtube.com/watch?v=9_ZkmZC1l_0

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary — столбец с зарплатами, а employees — таблица сотрудников в нашей базе данных */ SELECT AVG(salary) AS 'Средняя зарплата' FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */ SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты' FROM employees GROUP BY salary ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */ SELECT TOP(1) PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY salary) OVER() AS 'Медианная зарплата' FROM employees

Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при ании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Полезные ссылки:

Задача №6. Расчёт показателей вариации

По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:

Размер вклада, руб.

Число вкладчиков

До 400	400 — 600	600 — 800	800 — 1000	Свыше 1000
32	56	120	104	88

Определите:

1) размах вариации;

2) средний размер вклада;

3) среднее линейное отклонение;

4) дисперсию;

5) среднее квадратическое отклонение;

6) коэффициент вариации вкладов.

Решение:

Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.

Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.

Размер вклада, руб.

Число вкладчиков

200 — 400	400 — 600	600 — 800	800 — 1000	1000 — 1200
32	56	120	104	88

1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:

Размах вариации размера вклада равен 1000 рублей.

2) Средний размер вклада определим по формуле средней арифметической взвешенной.

https://www.youtube.com/watch?v=hFUUFFaPyFc

Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.

Среднее значение первого интервала будет равно:

второго — 500 и т. д.

Занесём результаты вычислений в таблицу:

Размер вклада, руб.Число вкладчиков, fСередина интервала, хxf

200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
Итого	400	—	312000

Средний размер вклада в Сбербанке города будет равен 780 рублей:

3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:

Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:

1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).

2. Определяются абсолютные отклонения вариант от средней:

3. Полученные отклонения умножаются на частоты:

4. Находится сумма взвешенных отклонений без учёта знака:

5. Сумма взвешенных отклонений делится на сумму частот:

Удобно пользоваться таблицей расчётных данных:

Размер вклада, руб.Число вкладчиков, fСередина интервала, х 

200-400	32	300	-480	480	15360
400-600	56	500	-280	280	15680
600-800	120	700	-80	80	9600
800-1000	104	900	120	120	12480
1000-1200	88	1100	320	320	28160
Итого	400	—	—	—	81280

Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.

4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

Расчёт дисперсии в интервальных рядах распределения производится по формуле:

Порядок расчёта дисперсии в этом случае следующий:

1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).

2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:

4. Умножают квадраты отклонений на веса (частоты):

5. Суммируют полученные произведения:

6. Полученная сумма делится на сумму весов (частот):

Расчёты оформим в таблицу:

Размер вклада, руб.Число вкладчиков, fСередина интервала, х

200-400	32	300	-480	230400	7372800
400-600	56	500	-280	78400	4390400
600-800	120	700	-80	6400	768000
800-1000	104	900	120	14400	1497600
1000-1200	88	1100	320	102400	9011200
Итого	400	—	—	—	23040000

5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:

6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:

По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

Средние показатели

Windows XP

Word 2003

Excel 2003

Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака статистической совокупности. Средние величины являются как бы «представителями» всего ряда наблюдений. Определить среднюю можно во многих случаях через исходное соотношение средней (ИСС) или ее логическую формулу:

.

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.

https://www.youtube.com/watch?v=SFMZWGa4T2I

Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1.

Понятие и виды средних величин

Средняя величина   — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

Существует 2 класса   средних величин:   степенные   и структурные .

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.

Степенные средние величины

Степенные средние могут быть простыми и взвешенными.

Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле средней степенной (при различной величине k (m)):

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

 где x- средняя величина исследуемого явления;

xi – i -й вариант усредняемого признака ;

        fi – вес i-го варианта.

где X – значения отдельных статистических величин или середин группировочных интервалов; m — показатель степени, от значения которого зависят следующие виды степенных средних величин: при m = -1 средняя гармоническая; при m = 0 средняя геометрическая; при m = 1 средняя арифметическая; при m = 2 средняя квадратическая;

при m = 3 средняя кубическая.

Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.

Средняя арифметическая

Средняя арифметическая – начальный момент первого порядка, математическое ожидание значений случайной величины при большом числе испытаний;

Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

 или

где X — значения величин, для которых необходимо рассчитать среднее значение; N — общее количество значений X (число единиц в изучаемой совокупности).

Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.

Средняя арифметическая взвешенная имеет следующий вид:

где f — количество величин с одинаковым значением X (частота).

>Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.

Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.

Например, на предприятии 10 работников со стажем работы до 3 лет, 20 — со стажем от 3 до 5 лет, 5 работников — со стажем более 5 лет. Тогда рассчитаем средний стаж работников по формуле средней арифметической взвешенной, приняв в качестве X середины интервалов стажа (2, 4 и 6 лет):

(2*10+4*20+6*5)/(10+20+5) = 3,71 года.

Функция СРЗНАЧ

Эта функция вычисляет среднее (арифметическое) своих аргументов.

СРЗНАЧ(число1; число2; …)

Число1, число2, …   — это от 1 до 30 аргументов, для которых вычисляется среднее.

Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения,  учитываются.

Функция СРЗНАЧА

Вычисляет среднее арифметическое значений, заданных в списке аргументов. Помимо чисел в расчете могут участвовать текст и логические значения, такие как ИСТИНА и ЛОЖЬ.

СРЗНАЧА(значение1,значение2,…)

Значение1, значение2,…   — это от 1 до 30 ячеек, интервалов ячеек или значений, для которых вычисляется среднее.

Аргументы должны быть числами, именами, массивами или ссылками. Массивы и ссылки, содержащие текст, интерпретируются как 0 (ноль). Пустой текст («») интерпретируется как 0 (ноль). Аргументы, содержащие значение ИСТИНА, интерпретируются как 1, Аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль).

Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.

Средняя гармоническая

Средняя гармоническая для определения средней суммы обратных величин;

Средняя гармоническая   применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

или

Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно — со скоростью 110 км/ч.

Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w1=w2   (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.

Функция СРГАРМ

Возвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин.

СРГАРМ(число1;число2; …)

Число1, число2, … — это от 1 до 30 аргументов, для которых вычисляется среднее. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

https://www.youtube.com/watch?v=kctXq60JNH4

Среднее гармоническое всегда меньше среднего геометрического, которое всегда меньше среднего арифметического.

Средняя геометрическая

Средняя геометрическая для оценки средних темпов роста случайной величин, нахождения значения признака, равноудаленного от минимального и максимального значения;

Средняя геометрическая применяется при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.

Например, в период с 2005 по 2008 годы индекс инфляции в России составлял: в 2005 году — 1,109; в 2006 — 1,090; в 2007 — 1,119; в 2008 — 1,133.

Так как индекс инфляции — это относительное изменение (индекс динамики), то рассчитывать среднее значение нужно по средней геометрической: (1,109*1,090*1,119*1,133)(1/4) = 1,1126, то есть за период с 2005 по 2008 ежегодно цены росли в среднем на 11,26%.

Ошибочный расчет по средней арифметической дал бы неверный результат 11,28%.

Функция СРГЕОМ

Возвращает среднее геометрическое значений массива или интервала положительных чисел. Например, функцию СРГЕОМ можно использовать для вычисления средних темпов роста, если задан составной доход с переменными ставками.

СРГЕОМ (число1; число2; …)

Число1, число2, …   — это от 1 до 30 аргументов, для которых вычисляется среднее геометрическое. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Средняя квадратическая

Средняя квадратическая – начальный момент второго порядка.

Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.

Главной сферой применения квадратической средней является измерение вариации значений X.

Средняя кубическая

Средняя кубическая– начальный момент   третьего порядка.

Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.

в начало

Средняя цена товара: как рассчитать, формула средневзвешенной цены

Средняя цена на товар или товарную группу — информативный и востребованный показатель при анализе хозяйственной деятельности торговой организации.

Особенно он значим в рознице — где различные «манипуляции» с ценами регулярны.

Исчисление средних цен в этом сегменте сейчас значительно облегчается благодаря оперативному доступу к первичным данным, которые находятся у заинтересованного лица прямо под рукой — на кассе предприятия.

Формулы средних цен

Средняя цена — показатель, который вычисляется в рамках анализа уровня цен на товар или товары, которые объединены в однотипные товарные группы. При сопоставлении средних цен за те или иные периоды (месяцы, кварталы, годы) можно подсчитать, к примеру, уровень инфляции — если говорить о макроэкономических задачах.

В бизнесе же вычисление средних цен может быть обусловлено, как вариант, подсчетом показателей хозяйственной эффективности — в сопоставлении со средними ценами конкурентов. Если выяснится, что у конкурентов при аналогичных средних ценах рентабельность выше, то значит, что в бизнес-модели исследуемого торгового предприятия что-то не так.

Аналогично средние цены применимы в контексте сравнения эффективности двух или нескольких магазинов одной розничной сети: применение показателя, о котором идет речь, позволит выявить наиболее прибыльную бизнес-модель в рамках соответствующих торговых точек.

https://www.youtube.com/watch?v=W7IbcLSN9o0

При этом есть несколько разновидностей средней цены. К числу наиболее часто применяемых относят нижеследующие.

Простая средняя арифметическая

Вычисляется она по формуле:

СРЕД (ПА) = СУММА (Цi) / СУММА (Оi),

где:

• Цi – цена на товар;
• Оi — объем товара, по которому считается средняя цена.

Простая средняя арифметическая применяется, если в распоряжении есть только 2 даты, на которые установлены анализируемые цены. Например — начало или конец месяца.

Средняя арифметическая взвешенная

Ее формула — следующая:

или простыми словами:

СРЕД (САВ) = СУММА (Ц * О) / СУММА О,

где:

• Ц — средняя цена за единицу товара за период реализации (месяц, квартал);
• О — объем реализованных товаров в тех или иных натуральных показателях (килограммах, литрах и иных) за все периоды реализации (за расчетный период — например, год).

Применяется рассматриваемая разновидность средней цены, если в распоряжении у статиста есть необходимые данные о ценах и объемах проданного товара за достаточно длительный период его реализации.

Средняя хронологическая

Вот ее формула:

или по-другому:

СРЕД (ХРОНОЛОГИЧ) = ((Ц1 / 2 + Ц2 + Ц3 + Ц4 + … + Цt / 2)) / t – 1,

где:

• Ц1, Ц2, Ц3, Цt – цены по состоянию на начало или конец месяца в расчетном периоде;
• t – количество месяцев в определенном периоде.

Рассматриваемая величина применяется, если в распоряжении статиста имеются сведения о ценах по состоянию на даты, между которыми промежутки времени — равные.

Средняя хронологическая взвешенная

Ее формула следующая:

или по-простому:

СРЕД (ХРОНОЛОГ ВЗВЕШ) = СУММА (Цсрi * ti) / СУММА ti,

где:

• Цсрi – средняя цена за расчетный период;
• ti – количество месяцев в расчетном периоде.

Средняя хронологическая взвешенная используется, если есть данные по неравным интервалам времени.

Средняя гармоническая взвешенная

Считается она по нижеследующей формуле:

или другими словами:

СРЕД (ГАРМОНИЧ ВЗВЕШ) = СУММА (Ц * О) / СУММА (Ц * О) / Ц),

где:

• Ц — цена товара за расчетный период;
• О — объем реализованного товара по соответствующей цене за отчетный период.

То есть, Ц * О — выручка за расчетный период по конкретному товару по конкретной цене.

Средняя гармоническая цена — хороша при анализе данных по товарам, реализованным на разных торговых точках за один и тот же период.

Рассмотрим практические примеры использования указанных видов средних цен.

Как рассчитать среднюю цену товара на примерах

Пример 1.

Надо определить среднюю цену 1 кг яблок по ценам реализации, действовавшим в течение года (в каждом из расчетных кварталов). Поскольку период подсчета средней цены — длительный, то будем считать среднюю арифметическую взвешенную цену.

Условимся, что мы продали:

• в 1-м квартале — 5000 кг яблок по цене 100 рублей за 1 кг;
• во 2-м квартале — 6000 кг яблок по цене 120 рублей за 1 кг;
• в 3-м квартале — 7000 кг яблок по цене 140 рублей за 1 кг;
• в 4-м квартале — 8000 кг яблок по цене 150 рублей за 1 кг.

Расчет средней арифметической взвешенной цены для данного примера:

СРЕД (ПА) = (5000 * 100 + 6000 * 120 + 7000 * 140 + 8000 * 150) / (5000 + 6000 + 7000 + 8000) = 130,77 рублей.

Пример 2.

Нужно рассчитать среднюю цену товара за 1-е полугодие, если в распоряжении есть фиксированные цены по состоянию на начало каждого месяца 1-го полугодия. В данном случае подойдет формула средней хронологической цены.

Условимся, что наш товар — груши, и мы устанавливали на них следующие цены:

• по состоянию на 1 января — 100 рублей за 1 кг;
• по состоянию на 1 февраля — 120 рублей за 1 кг;
• по состоянию на 1 марта — 140 рублей за 1 кг;
• по состоянию на 1 апреля — 145 рублей за 1 кг;
• по состоянию на 1 мая — 150 рублей за 1 кг;
• по состоянию на 1 июня — 155 рублей за 1 кг.

При этих условиях расчет средней хронологической цены выглядит так:

СРЕД (ХРОНОЛОГИЧ) = (100 / 2 + 120 + 140 + 145 + 150 + 155 / 2) / 6 — 1 = 136,5 рублей

Пример 3.

Нам надо рассчитать среднюю цену 1 кг яблок, которые реализованы на разных торговых точках. Лучше всего подойдет средняя гармоническая цена. Условимся, что мы продали:

• на точке А яблок на сумму 10 000 рублей по цене 100 рублей за 1 кг яблок;
• на точке Б яблок на сумму 12 000 рублей по цене 120 рублей за 1 кг яблок;
• на точке В яблок на сумму 15 000 рублей по цене 145 рублей за 1 кг яблок;
• на точке Г яблок на сумму 14 000 рублей по цене 150 рублей за 1 кг яблок.

Считаем требуемый показатель:

СРЕД (ГАРМОНИЧ ВЗВЕШ) = (10 000 + 12 000 + 15 000 + 14 000) / (10 000 / 100 + 12 000 / 120 + 15 000 / 145 + 14 000 / 150) = 128,53 рублей

https://www.youtube.com/watch?v=WUT5UuMRWTY

Применение указанных формул потребует наличия исходных данных. Рассмотрим, откуда их может взять современное торговое предприятие.

Где взять показатели для расчета

Сведения по ценам могут быть взяты:

1. Из традиционных источников — например, представленных регистрами цен в товароучетной системе.

Эти регистры сообщают статисту точную информацию — но не всегда знакомят его со сведениями о фактической реализации. Отражение таких данных в товароучетной платформе может быть не предусмотрено.

1. Из инновационных источников — записей:

Сведения фактически о каждом товаре, который отпускается через кассу, входят в состав фискальных данных, которые направляются в ОФД. Многие операторы формируют подробную аналитику по этим данным. В нее включаются, в частности, сведения о ценах по товарам, что были отпущены через онлайн-кассу.

Например, пользователь Яндекс.ОФД может ознакомиться с ценами на реализованные товары, что отражены в фискальных данных, заказав специальный отчет (заказываемый тип отчета — «Товары»). Составление отчета предполагается в привязке к каждой конкретной кассе.

Преимущество обращения к базам ОФД — в том, что там практически безошибочно отражены данные с учетом возвратов (которые, соответственно, снижают выручку — учитываемую, в частности, в формуле средней гармонической взвешенной цены). Дело в том, что во всех случаях возвраты включаются в фискальные данные.

Резюме

Средние цены — показатель, который может применяться как в макроэкономических исследованиях, так и на уровне финансового анализа деятельности отдельно взятого хозяйствующего субъекта. Исчислены они могут быть разными способами — в зависимости от состава вводных данных. Которые статист имеет возможность получить в том числе из отчетности ОФД по онлайн-кассам торгового предприятия.

Советуем посмотреть ПОДБОРКУ ПОЛЕЗНЫХ ОНЛАЙН-СЕРВИСОВ и ПО, которые будут полезны многим предпринимателям.

Звоните по телефону +7 (499) 348-19-87 (работаем во всех регионах РФ), если хотите узнать цены на ККТ, зарегистрировать кассу в ФНС, выпустить КЭП, подключить онлайн-кассу к ОФД.

Оборачиваемость товарных запасов

3. УРОВЕНЬ ЗАПАСОВ ПРОДУКЦИИ (УТЗ) – показатель, характеризующий обеспеченность магазина запасами на определенную дату, другими словами, на сколько дней торговли (при сложившемся товарообороте) хватит этого запаса :

Пример

На сколько дней хватит нам имеющегося запаса крема?

Утз = 243 шт. ( 180 дн. / 1701 шт. = 25,71.

На 25–26 дн.

Можно рассчитать оборачиваемость не в штуках или других единицах, а в рублях или другой валюте, то есть по стоимости. Но итоговые данные все равно будут коррелироваться между собой (разница будет только за счет округления чисел) – см. табл. 3.

Что дает оборачиваемость?

Основная цель анализа оборачиваемости запасов – определить те товары, у которых скорость цикла «товар–деньги–товар» минимальна, чтобы принять решение об их дальнейшей судьбе.

Для иллюстрации рассмотрим пример анализа коэффициента оборачиваемости двух товаров – хлеба и коньяка, являющихся частью ассортимента продуктового магазина (см. табл. 4 и 5).

Из данной таблицы видно, что хлеб и дорогой коньяк имеют совершено разные показатели – оборачиваемость хлеба в разы выше коньяка.

Но неправомерно сравнивать товары из разных товарных категорий – такое сравнение нам ничего не дает.

Очевидно, что у хлеба одна задача в магазине, а у коньяка – совершенно другая, и возможно, на одной бутылке коньяка магазин зарабатывает больше, чем от продаж хлеба за неделю.

Поэтому сравнивать между собой мы будем товары внутри категории – хлеб сравним с другими хлебными изделиями (но не с печеньем!), а коньяк – с другими элитными алкогольными продуктами (но не с пивом!). Тогда мы сможем сделать выводы об оборачиваемости товара внутри категории и сравнить его с другими продуктами, сходными по свойствам.

https://www.youtube.com/watch?v=pDzUDU7XT1Y

Сравнивая товары внутри категории, мы можем делать выводы о том, что у текилы период оборачиваемости больше, чем у того же коньяка, а интенсивность оборачиваемости меньше, и что виски в категории элитных алкогольных напитков имеют самую высокую оборачиваемость, а у водки (несмотря на то что ее продажи в два раза больше, чем у текилы) этот показатель меньше, что, видимо, требует корректировки складского запаса – возможно, завозить водку надо чаще, но более мелкими партиями.

Кроме того, важно отследить динамику изменения оборачиваемости в оборотах (Обр) – сравнить с прошлым периодом, с аналогичным периодом прошлого года: снижение оборачиваемости может свидетельствовать либо о падении спроса, либо о скоплении товаров плохого качества или устаревших образцов.

Оборачиваемость сама по себе ни о чем не говорит – нужно отслеживать динамику изменения коэффициента (Обр), учитывая следующие факторы:

• коэффициент уменьшается – идет затоваривание склада
• коэффициент растет или очень высокий (срок хранения меньше одного дня) – работа «с колес», что чревато отсутствием товара на складе

В условиях постоянного дефицита средняя величина складского запаса может быть равна нулю – например, если спрос все время растет, а мы не успеваем привозить товар и продаем его «с колес». В таком случае нет смысла считать коэффициент оборачиваемости в днях – возможно, его надо считать в часах или, наоборот, в неделях.

Если компания вынуждена хранить на складе товары нерегулярного спроса, товары с сильно выраженной сезонностью, то достижение высокой оборачиваемости – нелегкая задача.

Для обеспечения удовлетворенности клиента мы будем вынуждены иметь широкий ассортимент редко продающихся товаров, что будет тормозить общую оборачиваемость запасов. Поэтому расчет оборачиваемости по всем запасам в компании некорректен.

Правильно будет считать по категориям и по товарам внутри категорий (товарным позициям).

Также для магазина большую роль играют условия поставки товара: если закупка товара производится с использованием собственных средств, то оборачиваемость очень важна и показательна; если же в кредит, то собственные средства вы инвестируете в меньшей степени или не инвестируете совсем, тогда низкая оборачиваемость товаров не является критичной – главное, чтобы срок возврата кредита не превышал показатель оборачиваемости. Если же товар берется в основном на условиях реализации, то в первую очередь надо исходить из объема складских помещений, и оборачиваемость для такого магазина является последним по важности показателем.

Оборачиваемость и уходимость

Важно не путать два понятия – оборачиваемость и уходимость.

ОБОРАЧИВАЕМОСТЬ – это число оборотов товара за период.

УХОДИМОСТЬ – показатель, говорящий, за сколько дней товар уходит со склада Если при расчете мы оперируем не средним ТЗ, а подсчитываем оборачиваемость одной партии, то реально мы говорим об уходимости.

Норма оборачиваемости

Очень часто можно услышать вопрос: «А какие нормы оборачиваемости существуют? Как правильно?»

Коэффициент оборачиваемости не имеет рекомендуемых значений. Закономерность одна: чем он выше, тем меньше времени товары находятся на складе, тем быстрее они превращаются в деньги.

Но в компаниях всегда есть понятие «НОРМА ОБОРАЧИВАЕМОСТИ» и в каждой фирме она своя.
НОРМА ОБОРАЧИВАЕМОСТИ – это количество дней (или оборотов), за которые, по мнению руководства фирмы, должен быть реализован запас товара, чтобы торговлю можно было считать успешной.

В каждой отрасли – свои нормы. Некоторые компании имеют различные нормы для различных групп товаров. Так, например, наша торговая компания использовала следующие нормы (оборотов в год):

• строительная химия – 24
• лаки, краски – 12
• сантехника – 12
• панели облицовочные – 10
• рулонные напольные покрытия – 8
• керамическая плитка – 8

В одном из сетевых супермаркетов норма оборачиваемости по непродовольственной группе делится на основе АВС-анализа: для товаров А – 10 дней, для товаров группы В – 20 дней, для С – 30. В этой розничной сети закладывают в показатель товарного запаса месячную оборачиваемость, а товарный остаток по магазину складывается из нормы оборачиваемости плюс страховой запас.

https://www.youtube.com/watch?v=IHE4pRpi0eI

Так же некоторые специалисты по финансовому анализу пользуются западными нормами.

Как рассчитать средний коэффициент

24.07.2021

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии.

Для расчета стандартного отклонения используется функция СТАНДОТКЛОН.

Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака статистической совокупности. Средние величины являются как бы «представителями» всего ряда наблюдений. Определить среднюю можно во многих случаях через исходное соотношение средней (ИСС) или ее логическую формулу:

Расчет средних показателей

Если имеются только данные столбцов 1 и 3 , то известен знаменатель исходного соотношения, но не известен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность ППП. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:

Читать еще —>  Технический паспорт на квартиру реестровый номер

Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности варьируют под влиянием множества факторов, среди которых могут быть, как основные, так и случайные.

Сущность средней в том и заключается, что в ней взаимокомпенсируются отклонения значений признака, которые обусловлены действием случайных факторов, и накапливаются (учитываются) изменения, вызванные действием основных факторов.

Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Что показывает тарифный коэффициент

В Советском Союзе действовала единая тарифная сетка, в которой были установлены минимальные ставки (самого низкого квалификационного разряда для конкретной профессии) и ТК. Чем выше квалификация рабочего, трудоемкость работы, тем больше ТК, на который умножается минимальная ставка.

Тарифный коэффициент показывает, что оплата труда двух работников, выполняющих работу по одной и той же специальности (профессии) на одном и том же предприятии, может значительно различаться.

И причина этого — в разном уровне квалификации работников и сложности выполняемой ими работы.

В зависимости от квалификации и сложности работникам присваиваются разряды и устанавливаются тарифные коэффициенты (далее в статье — ТК).

Учимся вместе

Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину. В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.

https://www.youtube.com/watch?v=DW5-vfP1ezE

Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.

Читать еще —>  Получить субсидию на оплату жкх

В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот.

Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»).

Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).

Расчет средней арифметической в Excel

При вычислении среднего значения могут возникнуть ситуации, когда в расчет нужно включить не все значения, а только нужные, удовлетворяющие некоторым условиям (например, товары по отдельным товарным группам). Для этого есть готовая формула СРЗНАЧЕСЛИ.

Средняя арифметическая величина – один из наиболее часто используемых статистических показателей. Аналитику просто необходимо уметь использовать Эксель для ее расчета, а также для расчета других показателей. Да и вообще аналитик без виртуозного владения Эксель – самозванец, а не аналитик.

Как рассчитать средний коэффициент Ссылка на основную публикацию

💡 Видео