Что значит треть от общего числа

Учитель: Ребята, давайте представим, что к вам придут гости, и вас попросили положить на стол ложку, вилку, нож для каждого. Всего за столом будут сидеть 5 человек. Сколько предметов вам нужно взять? (Дети выходят к доске и предлагают свои варианты решения задачи)

Но ведь понятие 1/3 часть употребляется не только для математических расчетов. Когда есть три штуки — одна из этих трх и будет одной третью. Нужно что-то разделить на три равные части.

Когда нужно рассчитать 1/3 часть от чего-то, что не измеряется в штуках, — например quot;1/3 стакана — это сколько?quot; или quot;1/3 литра — это сколько?quot; — нужно стакан/ 1-литровую банку на глаз разделить на три части и набрать одну из этих 3-х частей.

Это например 3 часть стакана,к примеру говорю. Если стакан разделить на 2 части это будет 1/5-значит поровну.А 1/3 часть это треть этого стакана,нужно просто этот стакан разделить на равные 3 части.

В данном случае математическая дробь 1/3 означает деление целого на три части, и результатом этих действий является третья часть чего-либо. Причем при таком делении, целого числа мы не получим, а получим бесконечное выражение 0,333.

1/3 легко объяснить на стакане.

Делим стакан на три равные части и берем третью из них. Это и будет третья часть стакана.Так же можно поступить с любым другим предметом, из которого мы хотим использовать только третью часть.

Одна третья часть — это число деленное на три.Например:

Читать еще —>  1 сотка земли сколько в метрах

Что такое процент? Формула процентов

Согласно одной легенде, процент появился из-за глупой опечатки. Наборщик должен был выставить число 100, но перепутал и поставил так: 010. Это послужило причиной того, что первый ноль немного приподнялся, а второй опустился. Единица превратилась в обратный слеш. Такие манипуляции послужили тому, что появился знак процента. Конечно, есть и другие легенды о происхождении этой величины.

Калькулятор процентов

Кроме обозначения доли целого, проценты также используются для сравнения двух величин. При сравнении в процентах обязательно указывается относительно какой величины был вычислен процент. Например, доходы превышают расходы на 2% или цены на продукты повысились на 5% по сравнению с прошлым месяцем.

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Как найти процент от числа

NMitra Здравствуйте, платёж постоянный на протяжении всего срока или уменьшается с уменьшением основного долга? Проценты месячные или годовые? Я бы ориентировалась не на процент (какое-то число, например 20%), а на конечную сумму, которую вы отдадите банку помимо основного долга со всеми дополнительными комиссиями, в том числе единовременными:

Решение задач по математике онлайн

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Читать еще —>  Страховые взносы с выходного пособия при увольнении

Урок 1: общие сведения о дробях

В целое число можно превратить те неправильные дроби, в которых числитель либо равен знаменателю (об этом мы уже говорили, это будет «один»), либо делится нацело на знаменатель. Вот, например, тридцать шесть девятых. Равно тридцать шесть делить на девять. Равно четыре. Здесь все понятно.

https://www.youtube.com/watch?v=FJzgvQoimI8

В рассказе А. П. Чехова «Репетитор» гимназист Егор Зиберов не сумел решить арифметическую задачу, а отец репетируемого ученика, отставной губернский секретарь Удодов, пощелкав на счетах, получил правильный ответ.

Решите и Вы эту задачу арифметически? Вот она: Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он и того и другого, если синее стоило 5 руб. за аршин, а черное — 3 руб.

?

Доминикана привлекает треть от общего числа гостей центральноамериканского региона

Интересно, что если не обращать никакого внимания сквозь высокий спрос и большие суммы, вкладываемые особнякиниканой в свое продвижение на мировом рынке (около $50 миллионов), ежегодные темпы прироста потока любителей путешествовать по миру и вского рода злачным местам у нее сильно не очень-то вероятно, что должно хватить велики: всего 3,9%. При этом Панама, Никарагуа и Коста-Рика постоянно каждый год увеличивают число любителей путешаствовать в среднем на 9%.

Письмовник

Единственное и множественное число сказуемого

Выбор правильной формы числа сказуемого – трудная задача, если в составе подлежащего имеются слова, указывающие на количество или совокупность предметов. Среди таких слов:

• собирательные существительные (напр. большинство),
• количественные числительные (пять, двадцать),
• собирательные числительные (двое, трое, пятеро),
• счетные существительные (тысяча, миллион, миллиард),
• слова, обозначающие приблизительное количество (более десятка, менее пятидесяти, несколько),
• счетные местоименные наречия (много, столько, сколько),
• существительные со значением определенного (тройка, пара, сотня) и неопределенного (масса, уйма) количества, существительные с первой частью пол- (полгода, полдома),
• сочетания типа брат с сестрой.

Каждая из этих групп имеет свои особенности согласования со сказуемым.

Согласование сказуемого со словами  «ряд, большинство, меньшинство, часть, множество»

Выбор правильной формы сказуемого осложняется тем, что опорное слово подлежащего (ряд, большинство, множество и т. п.), представляя собой существительное в форме единственного числа,  фактически означает множество предметов или явлений как совокупность. В этой связи появляются две возможности для согласования сказуемого:

• формально-грамматическое согласование: сказуемое принимает такую же грамматическую форму, как и подлежащее; большинство граждан проало за нового президента («большинство» и «проало» – единственное число, средний род); ряд пользователей отказался от платной услуги («ряд» и «отказался» – единственное число, мужской род);
• согласование по смыслу: сказуемое принимает форму множественного числа, поскольку подлежащее обозначает множество предметов или явлений: большинство граждан проали за нового президента, ряд пользователей отказались от платной услуги.

В современном русском языке формально-грамматическое согласование сказуемого и согласование по смыслу конкурируют, и в большинстве случаев (но не всегда!) формы единственного и множественного числа сказуемого взаимозаменяемы. 

Формальное согласование рода и числа сказуемого требуется, если собирательное существительное не имеет при себе зависимых слов, а также если в составе подлежащего нет существительных в форме множественного числа: За принятие постановления проало большинство, меньшинство было против;Подавляющее большинство парламента проало против принятия закона; Часть населения безграмотна.

Согласование по смыслу предпочтительно:

1) если между подлежащим и сказуемым располагаются другие члены предложения: Множество замечаний по содержанию диссертации и оформлению библиографии были высказаны молодому аспиранту;

2) если при подлежащем имеется последующее определение в форме множественного числа, выраженное причастным оборотом или придаточным предложением со словом которые: Часть средств, вырученных от продажи книги, пойдут на содержание больниц; Часть средств, которые будут выручены от продажи книг, пойдут на содержание больниц;

3) если нужно подчеркнуть раздельность действий каждого действующего лица, называемого подлежащим, а также подчеркнуть активность действующих лиц: Ряд сотрудников нашей организации выступили с инициативой; ср.: В прошлом году было построено множество дорог.

4) если сказуемых – несколько: Ряд учеников не считают выполнение домашних заданий необходимым и приходят на урок неподготовленными.

5) если в составе сказуемого есть существительное или прилагательное в форме множественного числа: Большинство домов в этой деревне были деревянными.

Согласование сказуемого с числительными

Имя числительное, в отличие от других имен (существительного и прилагательного), лишено признаков числа. Иными словами, если существительные могут иметь формы единственного и множественного числа (книга – книги), то числительные не имеют таких форм (ср.: два, пятеро, сто пятьдесят).

По этой причине с числительным собственно «согласование» сказуемого по форме числа принципиально невозможно. Форма сказуемого единственного или множественного числа выбирается говорящим произвольно. При постановке сказуемого в ед. ч.

прошедшего времени сказуемое принимает форму среднего рода: пятьдесят человек пришло на лекцию, в ДТП погибло два человека; открылось десять новых магазинов и т. п.

https://www.youtube.com/watch?v=edtL8HsOEvc

Хотя форма сказуемого не регламентируется жестко, существует ряд факторов, способствующих употреблению формы единственного или множественного числа.

На постановку сказуемого в форму единственного числа влияет стремление автора текста обратить внимание читателей на пассивность подлежащего, совместность действия действующих лиц, а также на количество, названное в подлежащем. Пассивность подлежащего может подчеркиваться употреблением в качестве сказуемых глаголов со значением бытия, наличия: быть существовать, иметься и др.

В результате урагана упало двадцать деревьев. На лекцию пришло именно пятьдесят человек, а не пятьдесят два. У существительного имеется двенадцать падежных форм.

Факторы, способствующие употреблению формы множественного числа сказуемого, противоположны: значение раздельности действия,  акцент на активности лиц, названных в подлежащем, стремление автора обратить внимание на действие (характеристику), а не на количество. 

Восемь студентов уже защитили дипломные работы. Сто аспирантов пишут диссертации (т. е. каждый пишет собственную работу).

Кроме этого следует запомнить, что:

• Числительные, оканчивающиеся на один, обычно требуют формы единственного числа сказуемого: В институт поступил пятьдесят один абитуриент. Но: Пятьдесят один участник обсудили проблему на круглом столе (глагол обсудить означает совместное действие и не может быть употреблен в форме ед. ч.).
• Форма множественного числа сказуемого используется, если подлежащее конкретизируется определением в форме множественного числа, например словами все, эти, данные, любые и др. Все пятьдесят восемь абитуриентов поступили в институт. Васины пятьдесят рублей были немедленно потрачены. Эти двое явились с опозданием, остальные пятеро прибыли вовремя.
• Если числительное употребляется в качестве подлежащего без зависимых слов (обозначая число как математическое понятие), то оно согласуется со сказуемым в форме единственного числа: Сто пятьдесят делится на тридцать без остатка.

Согласование сказуемого со словами «тысяча, миллион, миллиард»

Сказуемое при словах тысяча, миллион, миллиард обычно принимает форму подлежащего (единственное число, женский или мужской род). Тысяча человек каждый год отдыхает в этом санатории. Миллион тюльпанов посажен на клумбе.

Согласование сказуемого при обозначении подлежащим приблизительного количества

При подлежащем – количественном сочетании со значением приблизительности предпочитается форма единственного числа сказуемого: Откроется несколько новых школ. На земле живет более трех миллиардов людей.  Но: Лишь несколько студентов смогли решить эту задачу; форма множественного числа сказуемого обусловлена  «активностью» действующих лиц, названных подлежащим.

Согласование сказуемого со словами «много, столько, немало»

Счетные местоименные наречия столько, сколько,много, немного, мало, немало согласуются иключительно со сказуемым в форме единственного числа: Столько долгов накопилось! Довольно много народу пришло на лекцию. Немало знаменательных событий предшествовало этому дню. Такое требование содержится в академической «Русской грамматике».

Д. Э. Розенталь в «Справочнике по правописанию и литературной правке» отмечает, что в последнее время форма множественного числа в подобных конструкциях «…встречавшаяся в прошлом редко, находит все большее распространение»: Сколько замученных работой калек помирают с голоду (М. Горький).

Согласование сказуемого с существительными со значением определенного («тройка, пара, сотня») и неопределенного («масса, уйма») количества, а также с числительным «пол-»

Существительные со значением определенного и неопределенного количества, а также слова с первой частью пол- (полчаса, полгода) обычно требуют постановки сказуемого в форму единственного числа: Пара ботинок была куплена за бесценок. Уйма времени ушла впустую. Масса ненужных вещей захламила квартиру. Полчаса прошло незаметно (но с определением: Первые полчаса прошли незаметно).

Согласование сказуемого с сочетаниями типа «брат с сестрой»

Сказуемое может стоять как в форме множественного, так и в форме единственного числа.

Форма множественного числа сказуемого показывает, что действие, обозначаемое сказуемым, в равной мере приписывается обоим действующим лицам, которые названы подлежащим.

Форма единственного числа сказуемого показывает, что обозначаемое сказуемым действие приписывается первому из названных действующих лиц. Ср.: Шарик с Матроскиным делят избу. Вася с мамой пошел в школу.

Академическая «Русская грамматика» отмечает, что «если в группу со значением совместности входит местоимение 1-го или 2-го лица, то глагол в сказуемом, уподобляясь числовому значению местоимения, имеет ту же личную форму, что и это местоимение: Я с отцом (с сестрами) пойду; Мы с отцом (с сестрами) пойдем; Ты с матерью (с сестрами) останешься; Вы с матерью (с сестрами) останетесь».

Данная статья написана по следам наиболее частых вопросов «Справочного бюро» ГРАМОТЫ.РУ и не претендует на полноту изложения. Подробные сведения о колебаниях в форме числа сказуемого читатели могут найти в «Русской грамматике» (М., 1980), параграфы 2244–2248.

Проценты

Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.

Что такое процент?

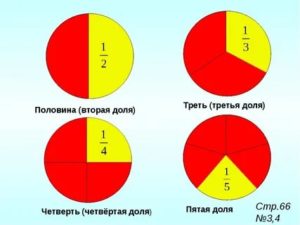
В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.

Процентом называется одна сотая часть чего-либо

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

https://www.youtube.com/watch?v=iM4R4jTZTmE

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

Найти    от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби 

Получили 0,1. Теперь 0,1 умножаем на числитель дроби 

0,1 × 2 = 0,2

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

0,2 см = 2 мм

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

300 : 100 = 3

Теперь полученный результат умножаем на 50

3 × 50 = 150 руб.

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись  . Тогда задание будет выглядеть так: Найти  от 300 рублей, а решать такие задачи для нас пока проще

300 : 100 = 3

3 × 50 = 150

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

1200 : 100 = 12

12 × 32 = 384

Ответ: 384 костюмов нового фасона выпустила фабрика.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись  , а если перевести эти  в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

300 × 0,5 = 150

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

https://www.youtube.com/watch?v=0wwf72ffQEg

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби.

Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби.

В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Задания для самостоятельного решения

Задание 2. Найдите 34% от числа 10501050 : 100 = 10,5
10,5 × 34 = 357 Задание 3. Найдите 25% от числа 8080 : 100 = 0,80
0,8 × 25 = 20 Задание 4. Найдите 185% от числа 1,51,5 : 100 = 0,015
0,015 × 185 = 2,775 Задание 5. Найдите 150% от числа 11501150 : 100 = 11,50
11,50 × 150 = 1725 Задание 8.

Представьте выражение 125% в виде обыкновенной дроби Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.12 : 60 = 0,2
0,2 × 100 = 20 Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2
2 × 100 = 200

Понравился урок?
Вступай в нашу новую группу и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Музыкальный размер: его виды и обозначения

Сегодня мы будем беседовать о музыкальном размере – числовом выражении метра, а также о том, как вести счет и дирижировать в различных размерах, но сначала немного повторим, что такое пульс, метр, сильные и слабые доли.

В предыдущем выпуске мы уже говорили о том, что основой музыки является равномерная пульсация. Удары пульса могут быть сильными и слабыми, причем сильные и слабые удары чередуются не как попало, а в какой-нибудь строгой закономерности.

Счет сильных и слабых долей

Чаще всего встречаются такие последовательности чередования: 1 сильный удар, 1 слабый или 1 сильный и 2 слабых. Для удобства удары пульса пересчитываются (рассчитываются на первый-второй или на первый-второй-третий, как на уроке физкультуры).

Причем каждый сильный удар является первым. В зависимости от количества слабых ударов счет ведется до двух, до трех или до другой величины, пока снова не наступит сильное время.

Такой счет ударов (их еще называют долями) называется музыкальным метром.

Предположим, что пульс бьется четвертными нотами, попробуем изобразить его биение в ритмической нотной записи. На нижеприведенном рисунке все удары пульса изображены четвертными нотами. Если удар сильный, то под ноткой стоит знак акцента (>), он похож на математический знак «больше».

Время от одной сильной доли до наступления следующей сильной доли в музыке называется тактом, такты разделяются, то есть отграничиваются друг от друга тактовой чертой. Таким образом, тактовая черта всегда располагается перед сильной долей, а это значит, что каждый новый такт начинается со счета «раз» (то есть с первой, сильной доли).

Какие бывают метры и такты?

Метры или такты бывают простыми и сложными. Простые – это двухдольные и трехдольные. А сложные – это такие, которые состоят из двух или нескольких простых. Причем соединяться могут как однородные метры (например, два трехдольных или два двухдольных), так и разнородные (смешиваются двухдольный и трехдольный).

Что такое музыкальный размер?

Музыкальный размер – это числовое выражение метра. Музыкальный размер измеряет наполняемость тактов (иными словами: сколько нот должно умещаться в один такт, в одну «коробку»).

Записывается размер обычно в виде двух чисел, которые по типу математической дроби располагаются одно над другим, только без черточки (без знака деления).

Примеры таких записей вы можете посмотреть на рисунке:

Что означают эти числа?

Верхнее число говорит о том, сколько всего долей в такте, то есть до скольких считать (до двух, до трех, до четырех, до шести и т.д.). Верхнее число следует произносить при чтении как имя числительное в женском роде и именительном падеже (то есть две, три, четыре, пять и т.д.)

Нижнее число показывает длительность каждой доли, то есть какими нотами нам считать и какими нотами вообще отбивается пульс (четвертными, половинными, восьмыми и т.д.). Нижнее число при чтении размера должно произноситься не как имя числительное, а как название соответствующей музыкальной длительности в родительном падеже.

https://www.youtube.com/watch?v=rdMPGuGCnD0

Примеры верных названий размеров: две четверти, три четверти, три восьмых, четыре четверти, шесть восьмых, три вторых (половинных – здесь исключение из правила), пять четвертей и т.д.

Простые музыкальные размеры

Простые музыкальные размеры образуются при простом метре, то есть эти размеры тоже будут или двухдольными, или трехдольными. Примеры простых размеров: две вторых, две четверти, две восьмых, две шестнадцатых, три вторых, три четверти, три восьмых, три шестнадцатых и т.д.

Размер 2/4 «две четверти» – это такой размер, в котором две доли и каждая доля равняется одной четвертной ноте. Счет ведется «раз-и, два-и». Значит, в каждом такте помещается по две четвертных ноты (ни больше и ни меньше). Но эти четвертные ноты, вернее их сумму, можно «набрать» разными длительностями.

Например, какую-то из долей или даже обе сразу можно раздробить на восьмые или шестнадцатые (можно в разных комбинациях), можно дробить на триоли и квинтоли. Также можно, наоборот, не дробить, а соединять две четверти в одну половинную, можно вписывать ноты с точками, используя знаки, увеличивающие длительности нот.

Вариантов ритмического рисунка в такте на две четверти может быть масса. Давайте посмотрим некоторые из них.

Размер 3/4 «три четверти» – в нем три доли, и каждая равна одной четвертной ноте. Счет ведется «раз-и, два-и, три-и». Сумму трех четвертей также можно набрать разными способами.

Если, например, объединить все три четверти в одну ноту, то получится половинная с точкой – это самая длинная нота, которую можно записать в такте с данным размером.

Посмотрите некоторые варианты ритмического заполнения для этого размера.

Размер 3/8 «три восьмых» – он похож на три четверти своей трехдольностью, только вот длительность каждой доли здесь восьмушка, а не четверть. Счет ведется «раз-два-три».

Восьмушка – основная длительность, но ее можно дробить на шестнадцатые при необходимости или соединять в четверти (если соединяются две восьмушки) или четверти с точкой (соединить сразу три восьмушки).

Распространенные варианты ритмического заполнения:

Сложные музыкальные размеры

Наиболее часто встречающиеся в музыке сложные размеры – это четыре четверти и шесть восьмых. Каждый из них состоит из двух простых.

Размер 4/4 «четыре четверти» – содержит четыре доли, и длительность каждой доли равна одной четвертной ноте. Этот размер сложился из суммы двух простых размеров 2/4, а значит в нем два акцента – на первой доле и на третьей.

Первая доля называется сильной, а третья, которой соответствует начало второго простого размера, называется относительно сильной, которая слабее, чем сильная.

Дополнительно сообщим, что музыкальный размер 4/4 иногда обозначают также знаком, похожим на букву C (незамкнутый круг).

Размер 6/8 «шесть восьмых» — это шестидольный размер, он сложен из двух простых трехдольных, пульсация идет восьмыми нотами. Сильная доля в нем первая, а относительно сильная – четвертая (начало второй простого размера 3/8).

Кроме этих самых распространенных сложных размеров, музыканту могут встретиться и другие, похожие на них: 4/8, 6/4, 9/8, 12/8. Все эти сложные размеры образованы по аналогичному принципу. Например, размер 9/8 – это три такта на 3/8 сложенные вместе, 12/8 – четыре таких же соединенных простых такта.

Смешанные размеры

Смешанные сложные размеры образуются, когда вместе соединяются не одинаковые, а разные простые, например, двухдольный с трехдольным.

Из многообразия смешанных размеров выделяются четыре, которые попадаются на глаза чаще остальных. Это 5/4 и 5/8, а также 7/4 и 7/8.

Время от времени музыкант может столкнуться и с размером 11/4, но это очень редко (например, в заключительном хоре «Свет и сила» из оперы «Снегурочка» Н.А. Римского- Корсакова).

Размеры 5/4 и 5/8 («пять четвертей» и «пять восьмых») – пятидольные, в их основе лежит один и тот же принцип, только в одном случае пульсация идет четвертными длительностями, а в другом – восьмушками. Так как эти размеры сложные, то они состоят из двух простых – двухдольного и трехдольного. Причем, возможны варианты данных размеров в зависимости от порядка следования простых.

Например, если в 5/4 сначала идет 2/4, а затем 3/4, то относительно сильная доля приходится на третью долю. Но если в том же размере вначале поставлен трехдольный, а после двухдольных, то в таком случае относительно сильная доля будет приходиться уже на четвертую долю, таким образом, будет смещен один акцент, и от этого изменится вся внутренняя ритмическая организация в такте.

https://www.youtube.com/watch?v=YzD8EVNjDMA

Для того чтобы исполнитель знал, с каким вариантом смешанного размера ему предстоит иметь дело, в нотах часто рядом с выставленным размером в скобочках указывается, из каких простых метров он сложен. По представленной сумме размеров обычно бывает понятно, что идет сначала – 2/4 или 3/4. Например: 5/4 (2/4 + 3/4) или 5/4 (3/4 + 2/4). То же касается и размера 5/8.

Размеры 7/4 и 7/8 – сложены из трех простых, один из которых трехдольный, а оставшиеся два – двухдольные. Такой размер чаще всего можно увидеть в обработках русских народных песен, иногда также в инструментальной музыке преимущественно русских композиторов.

Варианты сложения семидольного размера различаются местом положения трехдольного метра (чаще он располагается или в начале, или в конце такта, гораздо реже – в середине).

Имя числительное. Числительные в русском языке: порядковые и количественные

Имя числительное — это самостоятельная часть речи, которая обозначает количество, число или порядок предметов при счете. Числительное отвечает на вопросы сколько? какой? Который?

Примеры числительных в предложениях

Он подарил возлюбленной девять роз.

Мы живем в четвертом доме от метро.

Трижды три — девять.

По значению и грамматическим признакам имена числительные делятся на количественные и порядковые.

Количественные числительные обозначают количество или число и отвечают на вопрос сколько?
Сто человек. Двадцать ложек. Двенадцать миллиардов долларов.

Порядковые числительные обозначают порядок предметов при счете и отвечают на вопросы какой? какая? какое? какие?
Седьмой в очереди. Третий сын. Двухсотый номер.

Количество можно обозначить и другими частями речи.

Десяток яиц. Существительное.
Двойной эффект. Прилагательное.
Утроить выигрыш. Глагол.
Столько же людей. Местоимение.
Звонить дважды. Наречие.

Но если числительные можно записать цифрами, то другие части речи — лишь словами.

Простые, сложные и составные числительные

Простые числительные имеют единственный корень: один, два, три, шесть, пятнадцать, сорок, сто, тысяча.

Сложные числительные состоят из двух корней: шестьдесят, девяносто, двести, девятьсот.

Составные числительные складываются из нескольких слов: пятьдесят один, триста семнадцать, две тысячи триста тридцать пять.

Количественные числительные

Количественные числительные делятся на три разряда: целые числа, дробные числа и собирательные числительные.

• Целые числа: один, десять, семьдесят два, полтораста, тысяча пятьсот сорок один.
• Дробные числа: одна вторая, четыре пятых, семь восьмых.
• Собирательные числительные обозначает несколько предметов как одно целое: оба, трое, четверо, пятеро.

Количественные числительные не изменяются по числам, кроме слов один, тысяча, миллион, миллиард, триллион и т.п. Например: несколько миллиардов, мы были одни.

Категория рода является у этих числительных постоянным признаком.

Порядковые числительные

Порядковые числительные обозначают порядок предметов при счете. Обычно образуются от числительных, обозначающих целые числа: третий, десятый, сорок первый.

Порядковые числительные первый и второй не являются производными от чисел, это исходные слова.

Порядковые числительные, изменяются по падежам, числам и родам — как прилагательные.
Я первый.
Ты стал вторым.
Сказали третьему.

В составных порядковых числительных склоняется только последнее слово.
Мы будем в двадцать первом кабинете.
Походите к двадцать первому кабинету.

Синтаксическая роль числительного. Существительные с числительными

Числительное может быть любым членом предложения — подлежащим, сказуемым, определением, дополнением, обстоятельством.

https://www.youtube.com/watch?v=47m9s5kQOqQ

К нам подошли двое. Подлежащее.

Дважды два — четыре. Подлежащее и сказуемое выражены числительными.

Обоих зачислили в институт. Дополнение.

Зарплата выросла вдвое. Обстоятельства.

Пятый участник забега. Определение.

Числительные могут образовывать с именами существительными грамматически неделимые словосочетания. Такие сочетания являются одним членом предложения.

Двенадцать туристов вышли в поход. Подлежащее.

Мы высадили две клумбы. Дополнение.

Я прождал десять минут. Обстоятельство.

Порядковые числительные чаще всего бывают определением:
Попасть на пятый этаж можно на лифте.

Морфологический разбор имени числительного

I. Часть речи. Общее значение.

II. Морфологические признаки:

1. Начальная форма(именительный падеж).

2. Постоянные признаки:

а) простое или составное,

б) количественное или порядковое,

в) разряд (для количественных).

3. Непостоянные признаки:

а) падеж,

б) число (если есть),

в) род (если есть).

III. Синтаксическая роль.

Морфологический разбор числительного. Пример

За последний месяц я прочитал десять книг.

Десять — имя числительное, обозначает количество: прочитал (сколько?) десять (книг).Начальная форма — десять.Имеет морфологические признаки: .Постоянные: простое, количественное, обозначает целое количество.Непостоянные: здесь употребляется в винительном падеже.

В предложении входит в состав дополнения: десять книг.

Письменный разборДесять — числительноепрочитал (сколько?) десять (книг)н.ф. — десятьПост. признаки: колич., простое, целое количество;Непост. признаки: в В.п.

(что?) десять книг — дополнение.

Пословицы, поговорки и фразеологизмы с числительными

Беда не приходит одна.

Два сапога — пара.

Двум смертям не бывать, а одной — не миновать.

За одного битого двух небитых дают.

Тайна за семью печатями.

Конь о четырех ногах, и то спотыкается.

Лучше один раз увидеть, чем сто раз услышать.

Между двух огней.

Наглость — второе счастье.

Не имей сто рублей, а имей сто друзей.

Ноль без палочки.

Один в поле не воин.

Один за всех и все за одного.

Одна голова хорошо, а две — лучше.

От любви до ненависти — один шаг.

Первый блин комом.

Семеро одного не ждут.

Семь бед — один ответ.

Семь пятниц на неделе.

Семь раз отмерь, один раз отрежь.

Скупой платит дважды.

Старый друг лучше новых двух.

Убить двух зайцев.

Уплетать за обе щеки.

Читайте о других частях речи в русском языке

Существительное обозначает предмет.

Прилагательное — признак предмета.

Местоимение указывает на предмет.

Глагол обозначает действие.

Наречие — признак действия

Междометие передает восклицание, звук, эмоцию.

Количественные числительные

• Разряды
• Правописание количественных числительных
• Числительное ПОЛ

Количественные числительные – это слова, обозначающие числа и количества предметов. Количественные числительные отвечают на вопрос сколько?:

один, семь, сто пять.

Количественные числительные изменяются по падежам, но не изменяются по числам и родам. Исключение составляют числительные один, два, оба, полтора, которые изменяются по родам:

один – одна, два – две, оба – обе, полтора – полторы,

и числительные один, тысяча, миллион, миллиард, которые изменяются по числам:

один – одни, тысяча – тысячи, миллион – миллионы, миллиард – миллиарды.

Количественные числительные характеризуются специфической сочетаемостью с существительными:

• После числительного один (одна, одно) существительные стоят в именительном падеже единственного числа:

  один друг, одна чашка, одно дело.

  Числительное один согласуется с существительными во всех падежах:

  один друг, одного друга, одному другу, одним другом, об одном друге.

• После числительных два, три, четыре существительные стоят в родительном падеже единственного числа:

  два друга, три банана, четыре берёзы.

  После всех остальных числительных существительные стоят в родительном падеже множественного числа:

  семь друзей, сорок бананов, сто берёз.

  Во всех падежах, кроме именительного, числительные будут согласоваться с существительными:

  нет двух друзей, подошёл к двум друзьям, гордился двумя друзьями, говорил о двух друзьях.

Разряды

Количественные числительные делятся на разряды:

1. Целые (обозначают целое число):

   один, двадцать пять, сто.

2. Дробные (обозначают дробное число):

   три пятых, одна восьмая.

   Дробные числительные состоят из двух частей: первая часть – числитель дроби представляет собой количественное числительное в именительном падеже, вторая часть – знаменатель дроби представляет собой порядковое числительное в родительном падеже множественного числа: Если в числителе стоит 1 или 2, то употребляется форма женского рода:

   одна десятая, две седьмых.

   Дробные числительные пишутся раздельно.

   https://www.youtube.com/watch?v=H8uJDO_Rcbw

   В разговорной речи некоторые дробные числительные имеют определённые названия:

   одна вторая – половина, одна третья – треть, одна четвёртая – четверть.

   Существительные после дробных числительных всегда ставятся в родительный падеж единственного числа:

   половина яблока, три четвёртых площади, четверть килограмма.

   К дробным числительным относится и слово полтора, которое имеет всего две формы:

   М. и Cр. родЖ. родИ., В.
   Р., Д., Т., П.

   полтора	полторы
   полутора

3. Собирательные (всего 11 штук):

   двое, трое, четверо, пятеро, шестеро, семеро, восьмеро, девятеро, десятеро;

   о́ба (и тот и другой, и то и другое), о́бе (и та и другая).

   Собирательные числительные обозначают количество лиц или предметов как единую группу, что-то объединённое и нераздельное:

   обе сестры, четверо друзей.

   Собирательные числительные сочетаются:

   • С существительными, которые употребляются только во множественном числе:

     двое очков, трое санок.

   • С существительными мужского рода, обозначающими людей и детёнышей животных:

     трое друзей, пятеро котят.

     С этими существительными могут сочетаться и обычные количественные существительные:

     трое друзей – три друга, пятеро котят – пять котят.

   • С существительными, обозначающими парные предметы:

     двое носков, трое сапог.

   • С существительными женского рода сочетается только числительное обе:

     обе сестры, обе ноги.

   • С личными местоимениями:

     нас будет шестеро.

   После собирательных числительных, стоящих в именительном падеже, существительное ставится в родительный падеж множественного числа:

   двое мальчиков, трое котят, пятеро ребят.

   После собирательных числительных оба, обе, стоящих в именительном падеже, существительное ставится в родительный падеж единственного числа:

   оба мальчика, обе девочки.

   Числительные оба, обе единственные из собирательных, которые сочетаются с любыми существительными, обозначающими поддающиеся счёту предметы:

   оба окна, оба дела, обе двери, обе лапки.

Правописание количественных числительных

Количественные числительные, оканчивающиеся на -ДЕСЯТ, -СТА, -СОТ, пишутся слитно:

семьдесят, четыреста, девятьсот.

Числительное одиннадцать пишется с НН от выражения один-на-дцать, где -дцать обозначает десять.

Простые числительные от 5 до 10 и сложные числительные, которые заканчиваются на -ДЦАТЬ (от 11 до 20 и 30), пишутся с мягким знаком (Ь) на конце:

пять, тридцать.

При склонении данных числительных у них изменяются только окончания:

пять – пяти, тридцать – тридцати.

Сложные числительные, которые заканчиваются на -ДЕСЯТ (50 – 80) и на -СОТ (500 – 900), пишутся с мягким знаком (Ь) в середине:

семьдесят, семьсот.

При склонении изменяются обе части этих числительных:

семьдесят – семидесяти, семьсот – семистам.

Правописание мягкого знака в числительных

в серединена конце

пятьдесятшестьдесятсемьдесятвосемьдесятпятьсотшестьсотсемьсотвосемьсот девятьсот	пятьшестьсемьвосемьдевятьдесятьодиннадцатьдвенадцатьтринадцатьчетырнадцатьпятнадцатьшестнадцатьсемнадцатьвосемнадцатьдевятнадцатьдвадцать тридцать

Числительные триста и четыреста пишутся с А на конце. Числительные девяносто и сто в именительном и винительном падежах пишутся с О на конце, в остальных же падежах с А:

девяностостоИ.

Р.

Д.

В.

Т.

П.

девяносто	сто
девяноста	ста
девяноста	ста
девяносто	сто
девяноста	ста
о девяноста	о ста

Числительное ПОЛ

Вместо слова половина часто употребляется его сокращённая версия – пол. Числительное пол с другими словами может писаться слитно, раздельно или через дефис.

слитно

через дефис

раздельно

В составе сложных слов, вторая часть которых начинается с согласной буквы.	полвторогополчаса полстакана
В составе наречий.	вполухавполоборота вполголоса
Перед гласными буквами.	пол-яблока пол-арбуза
Перед согласной Л.	пол-лимона пол-литра
Перед именами собственными.	пол-Москвы пол-Италии
Если пол имеет самостоятельное значение и между ним и существительным стоит согласованное определение.	пол кофейной чашки пол третьего ночи

Новое на сайте	|	contact@izamorfix.ru
2021 − 2021	©	izamorfix.ru

💥 Видео